Representativeness is Rational When Memory is Limited

It makes sense to prioritize remembering stereotypical outcomes

TLDR: The representativeness heuristic is the tendency to think that outcomes are more likely when they’re more representative of the population that they come from. Though it’s often thought to be irrational, it may be the result of rationally organizing a limited memory.

---

Often reasoning that looks irrational turns out to be perfectly sensible given the fact that people have limited memories. In previous posts I’ve argued that this is true for both polarization and the gambler’s fallacy.

Today I want to focus on another case: the representativeness heuristic. This is— roughly—the tendency to think that an outcome is more likely if it is more representative (stereotypical) of the population from which it’s a part.

The classic examples are from Kahneman and Tversky 1972. They asked subjects, if a couple were to have 6 children, which sequence of gender assignments at birth is more likely:

• Boy, Girl, Boy, Boy, Boy, Boy

• Girl, Boy, Girl, Boy, Boy, Girl

Most subjects said the second is more likely than the first—despite the fact that, objectively, they’re about equally likely.¹ Representativeness explains this: the second sequence is more representative of the overall population than the first, since it’s closer to 50% boys and girls.

Similarly, when asked which of the following two sequences is more likely, most say that the second is:

• Boy, Boy, Boy, Girl, Girl, Girl

• Girl, Boy, Boy, Girl, Boy, Girl

The latter again seems more representative, since it switches more and is harder to summarize (or compress).

Final example: 20 marbles are distributed randomly amongst 5 children; which distribution is more likely?

• Jim: 4, Jane: 4, Joe: 4, Josiah: 4, Jill: 4

• Jim: 4, Jane: 4, Joe: 5, Josiah: 4, Jill: 3

Most people say the latter—even though the former is actually the most likely outcome. Intuitively, the reason people say this is that the latter looks more “(stereo)typical” of this sort of process: it has some apparent randomness and irregularity in it, as most outcomes do.²

It’s tempting to draw grand conclusions from these examples. If people think (stereo)typical outcomes are more likely than they actually are, maybe that explains the persistence of stereotypes, the misperception of political opponents, and the belief that outgroups are homogenous. Cue the nudges.

What is the representativeness heuristic?

What exactly does it mean to use the representativeness heuristic? It’s one of the most famous cases of apparent attribute substitution: substituting in a simple question in place of a complex one, and using the answer to the simple question as a guide to the complex one.

In this case, the complex question is:

• “What’s the probability of outcome X?”

and the simpler substitute is:

• “How similar is X to a typical X-type outcome?”

To answer the simple question, context must provide some metric (or collection of metrics) along which similarity can be judged. That is, there is some contextually-salient statistic S of the outcome which can be calculated, and people tend to favor outcomes that have a value of S that is close to a prototypical value of S in a large collection of outcomes.

In our first example, the statistic might be something like S = the proportion of boys. In the first outcome this is S[BGBBBB] = 5/6 ≈ 0.83; in the second sequence this is S[GBGBBG] = 3/6 = 0.5. Since in a large collection of births, the typical³ proportion of boys is very close to 0.5, the latter sequence is more representative.

In our second example, the statistic is something like, “How easy it is it to summarize (or compress) the sequence?”. In the third, the statistic is something like, “How uneven is the distribution of marbles?”

Or something like that. It’s hard to say precisely what the metric is in any given case—but you get the idea.

Why use the representativeness heuristic?

It’s standard to say that we use the representativeness heuristic because (1) similarity (on a given metric) is easier to calculate than probability, and (2) often similarity is a good enough guide to probability.

That answer is puzzling. Probability isn’t that hard—it’s just a way of counting proportions. Of course, counting proportions gets hard when there is a large number of dimensions along which things can vary, for then the number of proportions you need to keep track of blows up exponentially. This “curse of dimensionality” is why probability is computationally intractable. But the same goes for similarity!

There’s more to be said. But here I want to explore a different explanation for why people might tend to think representative outcomes are more probable than they actually are.

Proposal: With limited memory, it makes sense to prioritize remembering representative outcomes, since this will make your estimates about the overall outcomes more accurate.

In particular, we’re (likely) not going to remember all the outcomes we’ve seen. Given this, we have to figure out how (or whether) to prioritize remembering certain chunks of the data over others: if we’re going to forget some, which should we forget?

In a context where what we care about is having an accurate estimate about a given metric, it will make sense to remember chunks of the data that are representative of the overall data—for that means we’re more likely to forget the misleading parts of the data we’ve seen, and remember the parts that give us an accurate (i.e. representative) picture.

Let’s illustrate this with a toy model.

Forget children. Consider coin tosses.

Suppose we’ve seen a large sequence of (say, 100) tosses of a coin of unknown bias:

TTTTTHTTHHTTHTHTHTHTHHTTTHTTHHHHHTHHTTHTTTTTHHHTHTHHHTTTTHHHHTHTHTTHHHTHHHTTTHHTTTHTTTTHTHTHTHHTHHTH

We’d like to remember this as well as possible: have an accurate picture of what the overall sequence looks like, despite the fact that we might forget some parts of it.

Imagine you’re an agent whose memory works in the following simplistic way. First, you chunk the sequence into 10 chunks of 10:

TTTTTHTTHH    TTHTHTHTHT    HHTTTHTTHH HHHTHHTTHT   TTTTHHHTHT   HHHTTTTHHH  HTHTHTTHHH   THHHTTTHHT  TTHTTTTHTH   THTHHTHHTH

You have to figure out how to prioritize these various chunks in your memory: if you don’t remember them all, which do you remember?

In other words, you have to order them into a list of chunks {C1, C2, …., C10}. If you only remember one chunk, it’ll be {C1}. If you remember two, it’ll be {C1,C2}. If you only remember three, it’ll be {C1,C2,C3}. Etc.

Here are two natural ways you could order the chunks:

1. Naive Encoding: prioritize chunks by the order in which they appeared

2. Representative Encoding: prioritize chunks by how representative they are of the full sequence, on the salient metric X.

Suppose that later you’re going to be asked about the big sequence—for simplicity, suppose you know you’re going to be asked about the proportion of times it landed heads. (More realistically, there’ll be a range of statistics you might be asked about—a large enough range that it’s better to remember the actual chunks rather than just memorize statistics of the sequence, let’s say.)

To answer that question, you’re going to recall as many chunks as you can, and then use the features of the chunks you’ve recalled to estimate the features of the overall sequence.

Fore example, suppose you use Naive Encoding and recall the first 5 chunks. Then you’ll recall:

TTTTTHTTHH    TTHTHTHTHT    HHTTTHTTHH HHHTHHTTHT   TTTTHHHTHT

The proportion of heads in this subsequence is 22/50 = 0.44. Meanwhile, the true proportion of heads in the full sequence above is 48/100 = 0.48, so your estimate misses by 0.44-0.48 = -0.04, and your squared error is (0.44–0.48)^2 = 0.0016.

Suppose instead you had done Representative Encoding. Then you’d have re-ordered the chunks in terms of how close each chunk was to the overall proportion heads—namely, to 0.48.

Notice, for example, that the first chunk (TTTTTHTTHH) has only 3/10=0.3 proportion heads, while the third (HHTTTHTTHH) has 5/10=0.5. Since the latter is closer to the overall proportion (0.48), Representative Encoding will prioritize it over the former.

Re-ordering the chunks in terms of representativeness yields this ordering:

THHHTTTHHT HHTTTHTTHH TTTTHHHTHT TTHTHTHTHT THTHHTHHTH HTHTHTTHHH HHHTTTTHHH HHHTHHTTH TTTTTHTTHH TTHTTTTHTH

Given this ordering, if you remember the first 5 chunks (the ones in bold), you’ll estimate an overall proportion of heads at 24/50=0.48—your estimate is spot on.

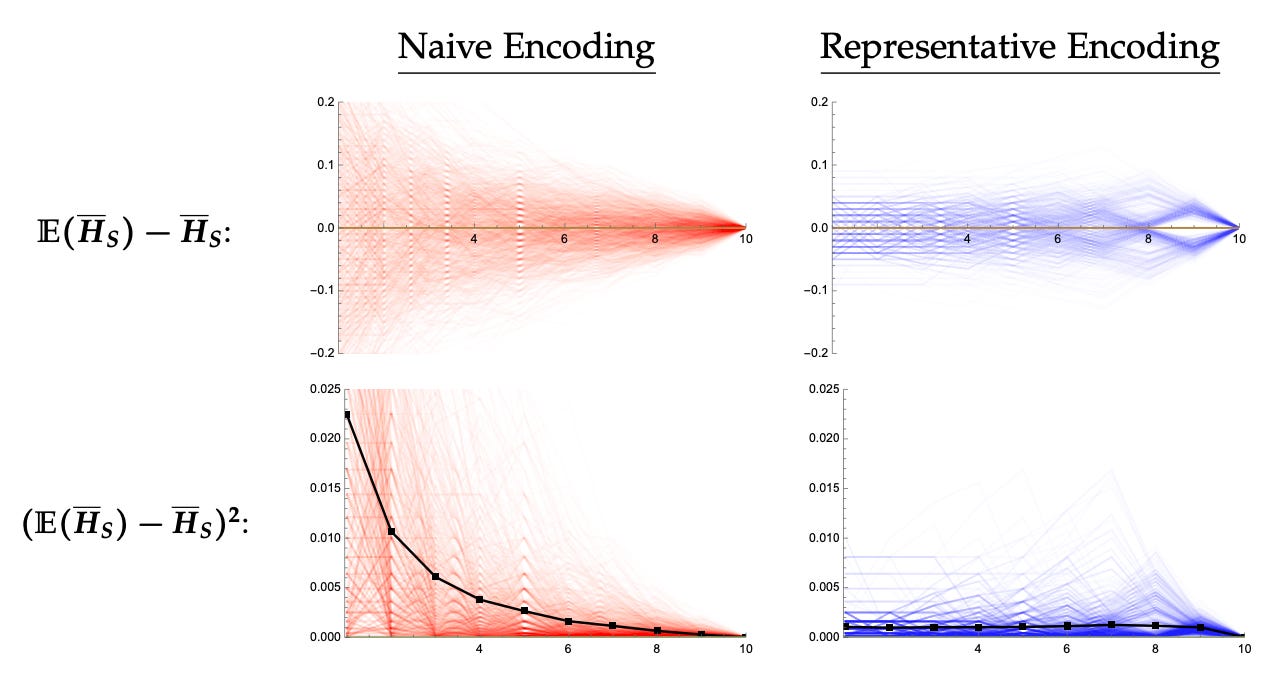
This generalizes. Suppose we randomly generate sequences of length 100, have you remember different numbers of chunks, and then record both (1) how far your estimate was from the true proportion, and (2) what its squared-error was.

The results of using Naive Encoding are in red on the left; the results of using Representative encoding are in blue on the right. The top row shows how far off your estimate is from the true proportion as a function of how many chunks you remember (the x-axis); the bottom rows show your squared error as a function of how many chunks you remember (the black line is the average):

As you can see: unless you almost always remember almost all the chunks, Representative Encoding leads to much more accurate estimates than Naive Encoding.

Upshot: given limited memory, it might make sense to prioritize remembering representative (or stereotypical) outcomes.

What follows?

How does Representative Encoding lead to the representativeness heuristic—i.e. judging that representative outcomes are more likely?

Consider what will happen when you survey your memories to figure out what a typical sequence looks like. Since you’ve prioritized remembering representative sequences, representative outcomes appear be more common than they actually are (and unrepresentative outcomes appear less common than they actually are).

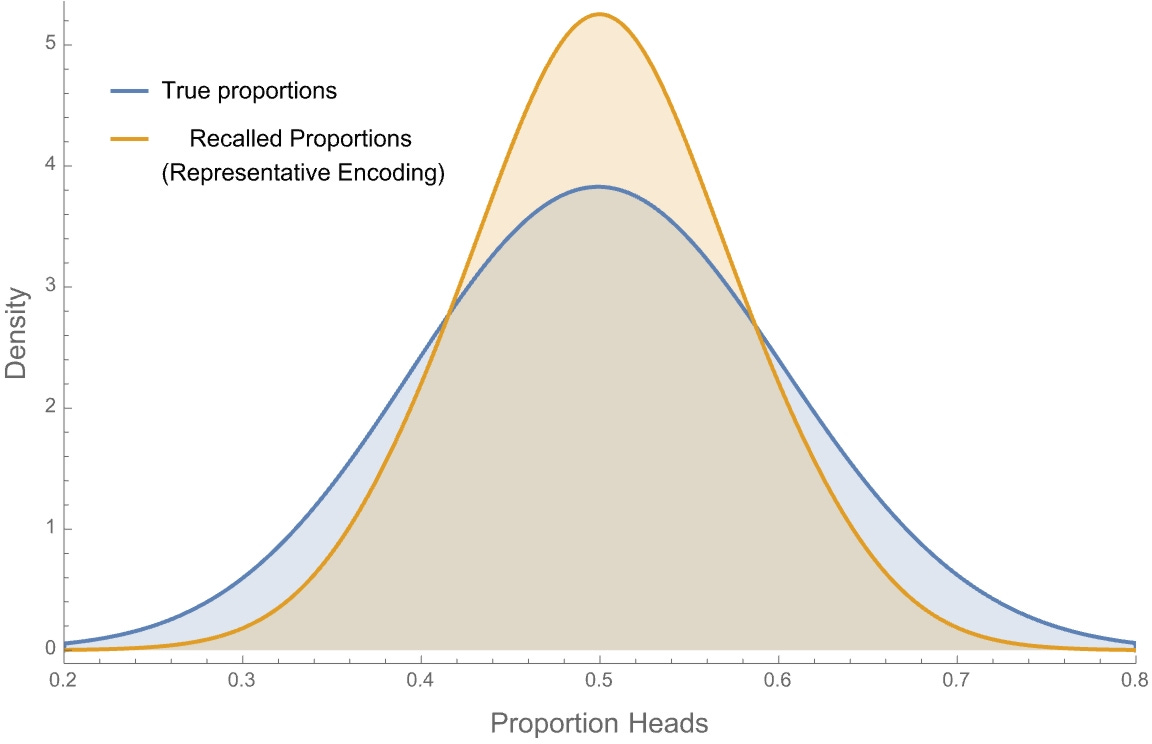
For example, suppose our Representative-Encoder recalls a bunch of 30-toss sequences from their memory—i.e. cases where they remembered 3 chunks of 10. How common will various proportions of heads be in those sequences? Here are density plots for how common various proportions truly are (blue) versus how common they are in representative-encoded memory (orange):

Although they have the same shape, representative memory exaggerates the trends: common proportions (near 50%) appear more common than they actually are, while uncommon ones (below 40% or above 60%) appear less common than they actually are.

That means Representative Encoding can explain the evidence for the Representativeness heuristic. Rather than using similarity as a proxy for probability—as is standardly assumed—representativeness may instead correlate with priority in memory. A natural consequence is that when we try to estimate probabilities by sampling from our memories, we end up over-weighting representative outcomes.

For example, when you were asked which of the following sequences of births is more likely, perhaps your (unconscious) memory finds more gender-ratio-representative families (like the second) than gender-ratio-unrepresentative families (like the first):

• Boy, Girl, Boy, Boy, Boy, Boy

• Girl, Boy, Girl, Boy, Boy, Girl

That would explain why it’s common to think that the second is more likely.

Upshot: rather than an instance of attribute substitution, the empirical trends that support the representativeness heuristic may be a side effect of an adaptive use of limited memory. Since rationality is doing the best you can, given your (memory and other) limits, maybe it’s not irrational after all.

1. If anything, the first should be more likely since boys are slightly more likely at birth than girls.

2. Although (4,4,4,4,4) is the most common outcome, there’s only one way to have an exactly uniform distribution, while there are many ways to slightly deviate from it. The probability of (4,4,4,4,4) is roughly 0.3%, while that of (4,4,5,4,3) is roughly 0.25%; but the probability of “deviates only 1 from uniform” (i.e. “(5,3,4,4,4) or (5,4,3,4,4) or…”) is about 10.1%.

3. What do expounders of the representativeness mean by “typical” large collection here? I’m really not sure—it’s natural to read it as “likely”, but then it’s less clear whether similarity is really replacing probability. Perhaps the thought is that we can have a single pre-loaded prototype of what a likely big collection of outcomes would look like; then the representativeness heuristic lets us reduce many different individual probability judgments to individual similarity judgments to a single, re-used probability judgment? I’m really not sure. What do you think?