Rational Bayesians Don’t Converge to the Truth

Why small memory lapses add up

TLDR: It’s common to think: “Rational people—or, at least, rational experts—will converge to the truth. So people who don’t converge to the truth or don’t defer to experts must be irrational or dogmatic.”  This is wrong. Rational people with imperfect memories don’t converge and shouldn’t be deferred to.

---

Here’s an argument I come across a lot:

Rational people would think like ”Bayesians”. And—given enough evidence—Bayesians pretty much always converge to the truth.  So since people often don’t agree on the truth (think: politics, religion, economics) even though there’s a ton of evidence, people aren’t Bayesian—so aren’t rational.

A  related argument goes like this:

We should expect experts to form rational opinions on their topic of expertise. That means we should expect them to converge to the truth, and therefore should defer to their opinions. So people who don’t defer to the experts are being irrationally dogmatic.

I think both of these arguments are wrong for lots of subtle reasons.  But today let’s focus on a simple one:

Given any memory limits at all, otherwise perfectly rational Bayesians will not usually converge to the truth. 

Since real people do have serious memory limits, then even if they are approximately Bayesian, (1) it’s no surprise that they don’t converge, and (2) since the same applies to experts, refusal to defer is often reasonable.

How does this work?  Start with a perfect Bayesian: someone who’s beliefs at any given time are probabilistic (can be represented with a single probability function), and who always updates by conditioning on their total evidence.  Provided there’s enough evidence around and they’re sufficiently open-minded, such agents will always converge to the truth.

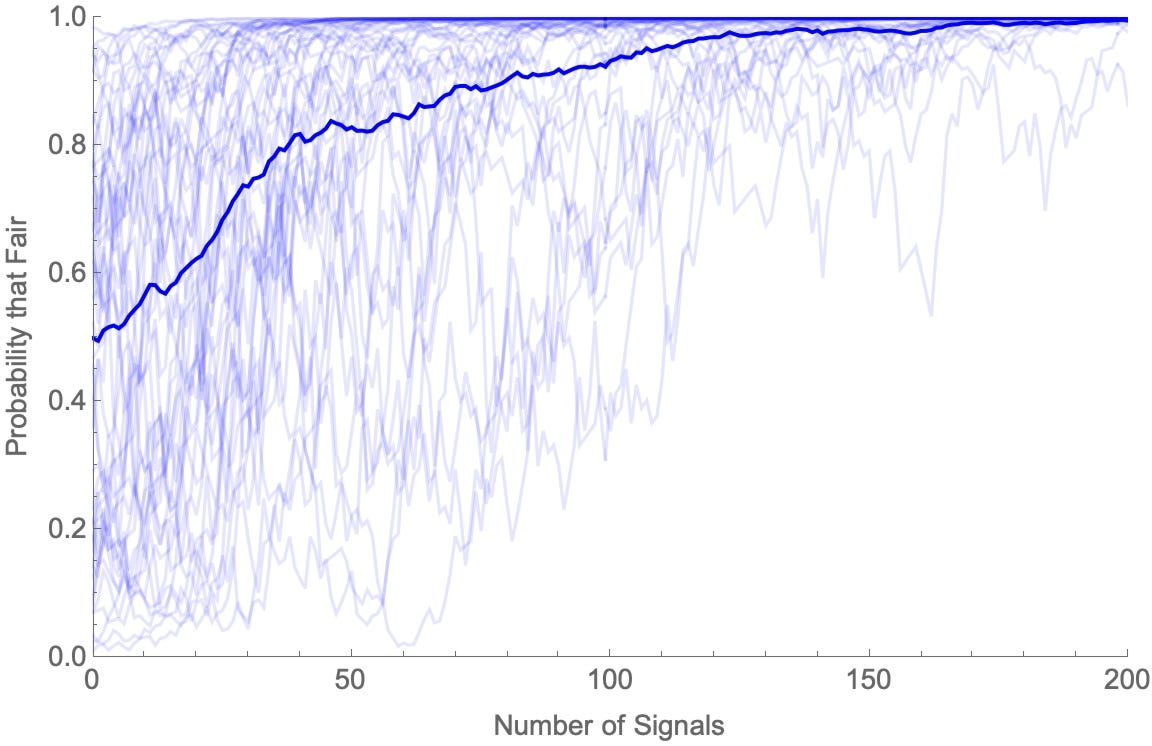
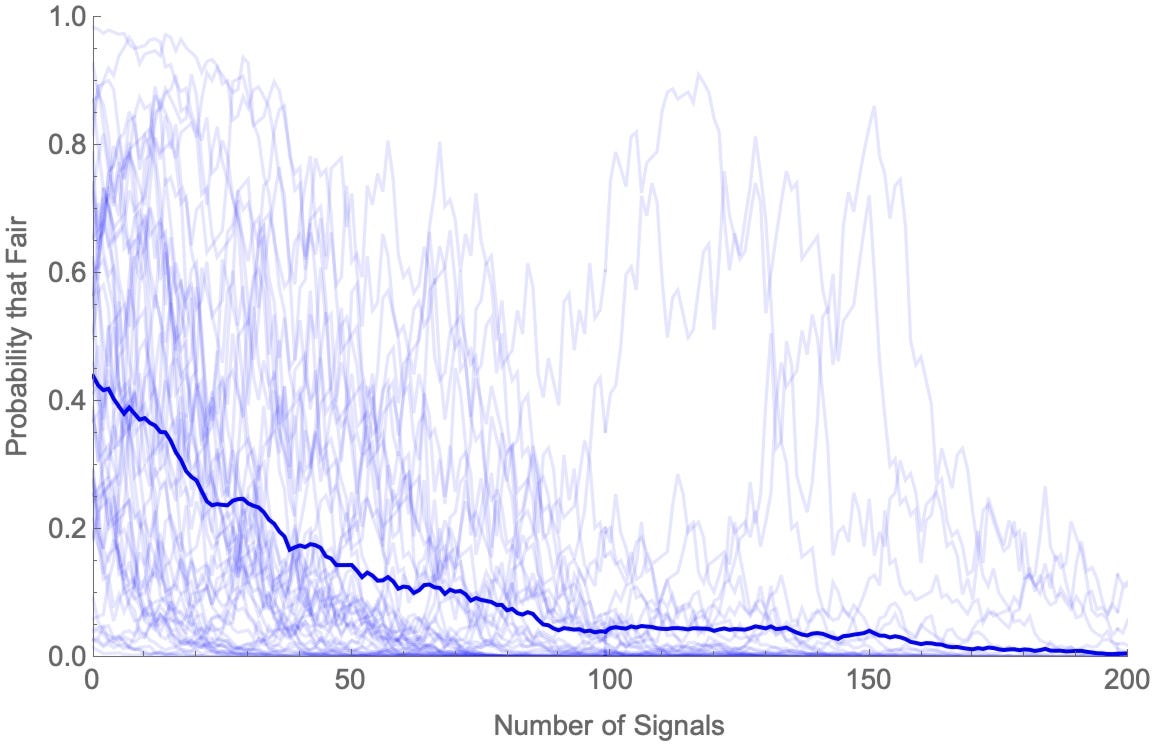
Consider a simple example.  I’ve got a coin which could either be fair or could be biased to only land heads 45% of the time; a group of Bayesians (all starting with different priors about the coin) are unsure which.  Each agents tosses the coin 10 times and then conditions on the exact proportion of times it landed heads. They each repeat 200 times.  This’ll be enough for them to converge.

Here are their beliefs (“How likely is the coin fair” over time on a given simulation run (thin lines are individuals; thick line is their average). 

If the coin is fair:

If unfair:

But these agents have perfect memories.  If you only ever update by conditioning, then whenever you learn something you become certain of it, and never lose that certainty. It follows that if asked how the coin landed on the 234^th toss seen, they know the answer with certainty.

Obviously real people aren’t like that.  What if we consider agents who can’t keep track of everything, but otherwise behave like perfect Bayesians? For example, what if sometimes they can’t recall the exact number of heads. If they got 5 heads out of 10 tosses, then after seeing the sequence (or, if you like, some time later) all they can recall is “either 5 or 6 heads”.  (Or, sometimes, “Either 4 or 5 heads”).  Then the group needn’t converge.

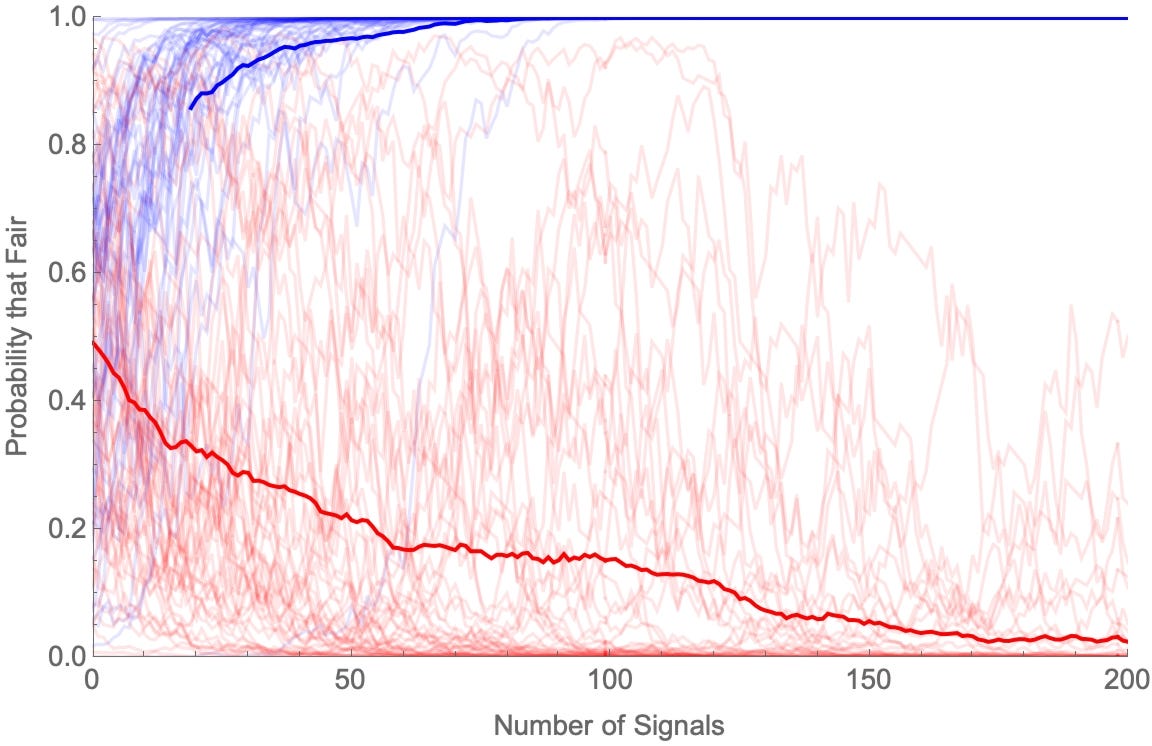
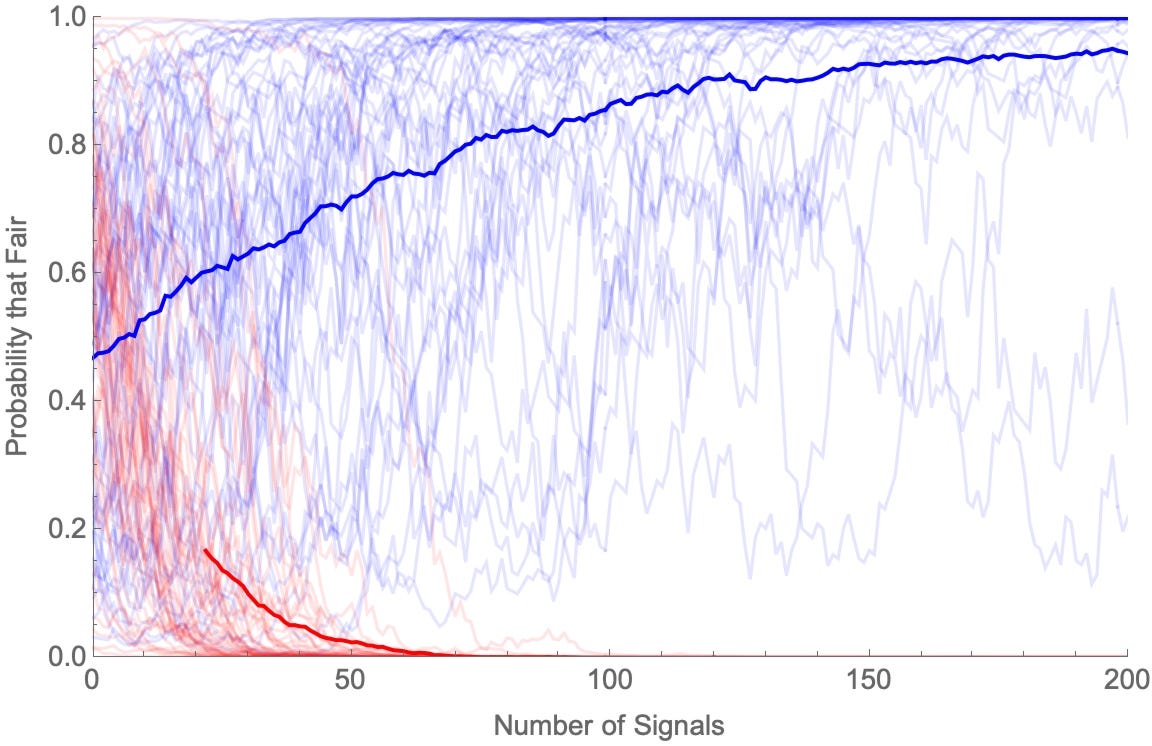
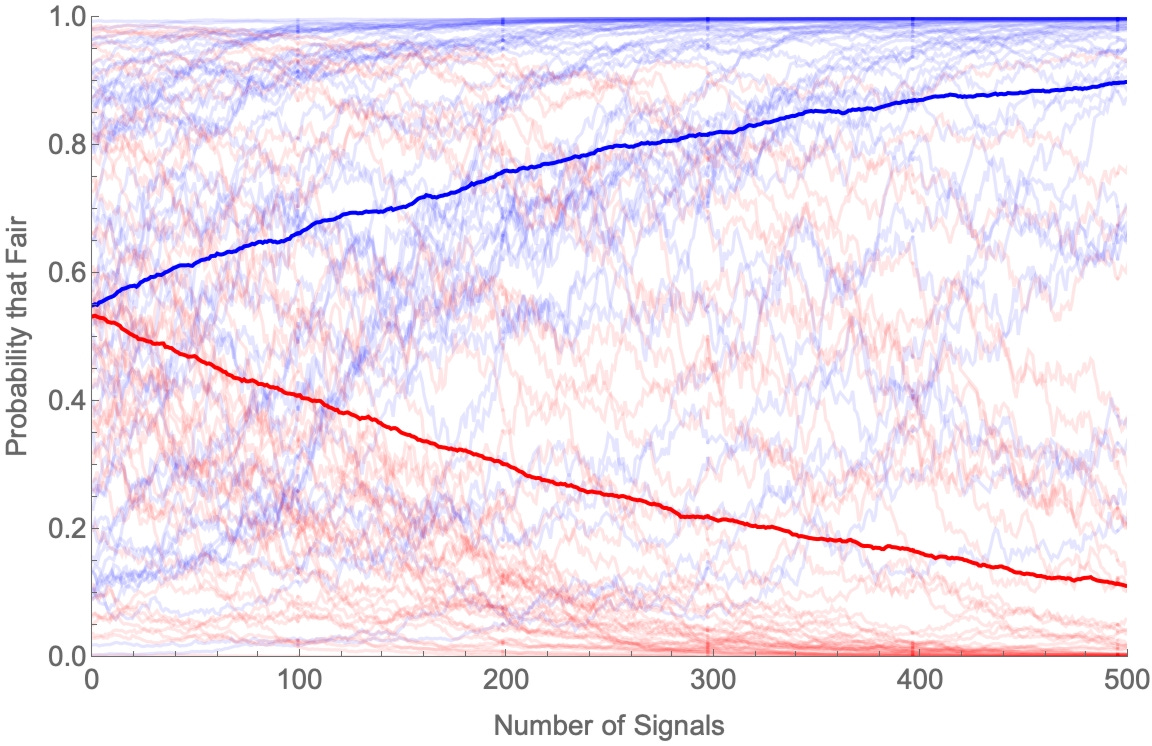
Start simple.  One group (Blues) is more inclined to forget in the higher-proportion-heads direction, other other (Reds) is more inclined to forget in the lower-proportion-heads direction.  That is: when the coin lands heads n times, Blues remember “n or n+1 heads”, while Reds remember “n-1 or n heads”.  Then we get diverging opinions.

When the coin is fair:

And when it’s biased:

Nothing turns on having such a neat bifurcation of the population.  Suppose instead each agent has a random memory tendency: with probability p (pulled uniformly from [0,1] for each agent), when they see n heads they remember “either n or n+1 heads”, and with probability 1–p they remember “n-1 or n heads”.  Then the population will naturally split.

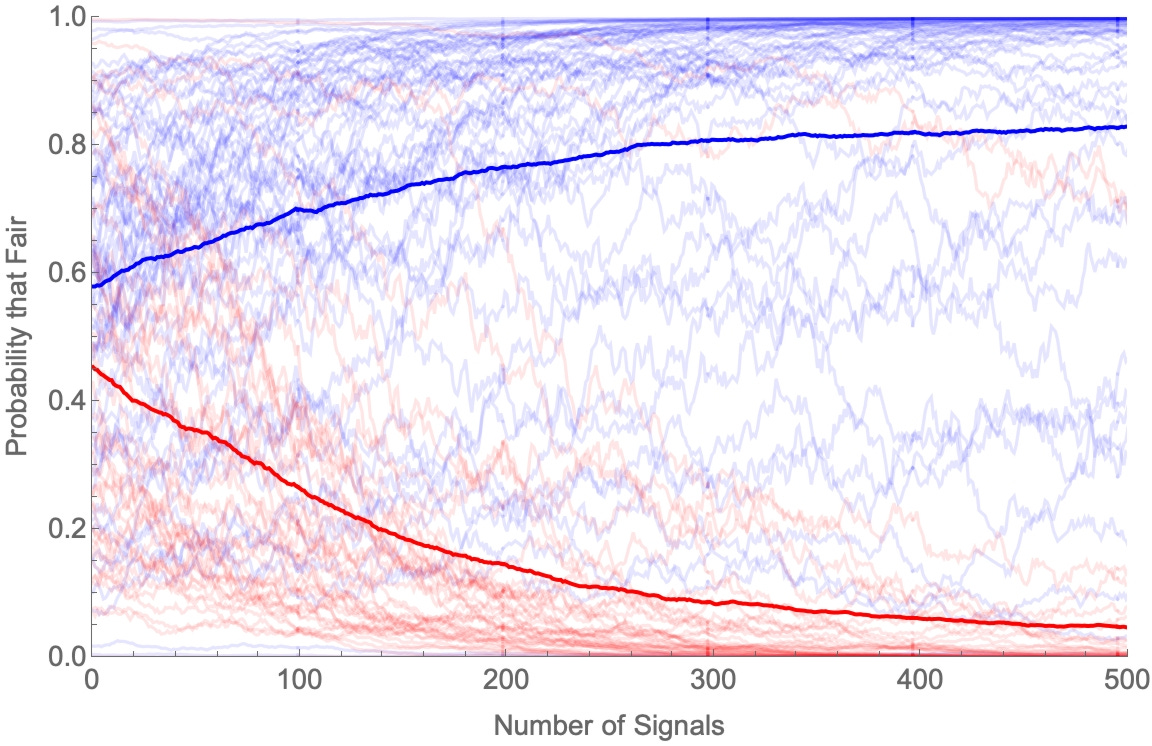
It’s easier to see this if we make the task harder: suppose the coin is either fair (50% likely to land heads), or slightly biased for tails (49% likely to land heads).  Then if we color agents as Blue if they are more likely to remember higher numbers (p > ½), and Red if they’re more likely to remember lower numbers (p<½), the population naturally diverges into camps.

If the coin is fair:

If the coin is biased:

What does this mean?  

Our two arguments are wrong.

The first argument said polarization was evidence for irrationality. But we know that people don’t have perfect memories.  So even if they’re otherwise rational, if they have variations in their memory dispositions, we should expect disagreement and polarization on hard questions.  So polarization is not evidence for irrationality—it’s exactly what we’d expect from memory-limited rational people.

The second argument said experts should be expected to converge, so failure to defer to experts is a sign of irrationality.  But we also know that experts have imperfect memories and can’t keep track of all the data. As a result, if we have beliefs about the direction in which their memory is selective, we shouldn’t often defer to them.  

In our simulations, here’s how this works. Suppose I’m 50-50 that the coin is fair, and you tell me that a smart person has looked at a ton of evidence on the issue, and concluded that the coin is at least 90% likely to be fair.  Should I “defer” to this expert, and become at least 90% confident the coin is fair myself?

Not if I think they have selective memory or attention.  The question for me is: how strong evidence is the expert’s belief that the coin is fair for the claim the coin is fair?  As a Bayesian, that depends on how much I should expect them to believe this on the two possible hypotheses—that is, how likely they’d believe it’s fair if it is fair versus how likely they’d believe it’s fair if it’s biased. Precisely:

• P(they’re at least 90% in fair | fair), versus

• P(they’re at least 90% in fair | biased)

If the latter is high enough—I believe they’d think it’s fair even if it wasn’t fair—then their “expert” belief is extremely weak evidence that the coin is fair.

For example, suppose I know their probability of remembering higher numbers (if n, they remember “either n or n+1”) is between 0.8 and 1, and I know they’ve looked at 500 sequences of 10 tosses each.

Then conditional on it being fair, I’m 99% confident they’d have this opinion: P(they’re at least 90% in fair | fair) = 0.99.  But conditional on it being biased, I’m still 96% confident that they’d have this opinion: P(they’re at least 90% in fair | biased) = 0.96.

So the information I got—that this expert is at least 90% confident the coin is fair—is actually extremely weak evidence: it should only move my belief from 50% to 51% confidence the coin is fair.

Upshot: since we know even experts have selective memories, we should often be skeptical of expert consensus.  In a world full of hard problems and imperfect memories, rational experts are often wrong.

What next?

• For more on the limits of Bayesian convergence, see this recent paper by Nielsen and Stewart.

• For the effects of ambiguous evidence on Bayesian convergence—with different models of ambiguity—see this paper and this one.

• For other models of memory limits, see this fantastic paper by Andrea Wilson and this one by Dan Singer and others.