Ideological Bayesians
Why limits on attention can lead reasonable people into bias and polarization.
TLDR: It’s often said that Bayesian updating is unbiased and converges to the truth—and, therefore, that biases must emerge from non-Bayesian sources. That’s wrong. For agents like us, updating on our total evidence is impossible—instead, we must selectively attend to certain questions, ignoring others. Yet correlations between what we see and what questions we ask—“ideological” Bayesian updating—can lead to predictable biases and polarization.
Professor Polder is a polarizing figure.
His fans praise him for his insight; his critics denounce him for his aggression.
Ask his fans, and they’ll supply you with a bunch of instances when he made an insightful comment during discussions. They’ll admit that he’s sometimes aggressive, but they can’t remember too many cases—he certainly doesn’t seem any more aggressive than the average professor.
Ask his critics, and they’ll supply you with a bunch of instances when he made an aggressive comment during discussions. They’ll admit that he’s sometimes insightful, but they can’t remember too many cases—he certainly doesn’t seem any more insightful than the average professor.
This sort of polarization is, I assume, familiar.
But let me tell you a secret: Professor Polder is, in fact, perfectly average—he has an unremarkably average number of both insightful and aggressive comments.
So what’s going on?
His fans are better at noticing his insights, while his critics are better at noticing his aggression. As a result, their estimates are off: his fans think he’s more insightful than he is, and his critics think he’s more aggressive than he is. Each are correct about individual bits of the picture—when they notice aggression or insight, he is being aggressive or insightful. But none are correct about the overall picture.
This source of polarization is also, I assume, familiar. It’s widely appreciated that background beliefs and ideology—habits of mind, patterns of salience, and default forms of explanation—can lead to bias, disagreement, and polarization. In this broad sense of “ideology”, we’re familiar with the observation that real people—especially fans and critics—are often ideological.1
But let me tell you another secret: Polder’s fans and critics are all Bayesians. More carefully: they all maintain precise probability distributions over the relevant possibilities, and they always update their opinions by conditioning their priors on the (unambiguous) true answer to a partitional question.
How is that possible? Don’t Bayesians, in such contexts, update in unbiased2 ways, always converge to the truth, and therefore avoid persistent disagreement?
Not necessarily. The trick is that which question they update on is correlated with what they see—they have different patterns of salience. For example, when Polder makes a comment that is both insightful and aggressive, his fans are more likely to notice (just) the insight, while his critics are more likely to notice (just) the aggression. This can lead to predictable polarization.
I’m going to give a model of how such correlations—between what you see, and what questions you ask about it—can lead otherwise rational Bayesians to diverge from both each other and the truth. Though simplified, I think it sheds light on how ideology might work.
Limited-Attention Bayesians
Standard Bayesian epistemology says you must update on your total evidence.
That’s nuts. To see just how infeasible that is, take a look at the following video. Consider the question: what happens to the exercise ball?
I assume you noticed that the exercise ball disappeared. Did you also notice that the Christmas tree gained lights, the bowl changed colors, the blanket became a sweatshirt, and about a dozen other things changed too? I doubt it.
In some sense, of course, the entire visual scene was part of your evidence—for any particular question about it (“Is there an exercise ball? Christmas tree? Bowl?”), you could answer that question. But—even in a static visual scene—there are far too many such questions to answer them all. Only a small fraction of the answers can be explicitly noticed and encoded in memory.
This is an instance of the epistemological point that we need to classify our experiences: we need concepts and habits of mind to make sense of the “blooming, buzzing confusion” that constantly confronts our senses.
Let’s put this into a simple model.
Bayesians usually say that evidence comes in as the true cell of a partition—a set of mutually exclusive, collectively exhaustive ways the world could be. Intuitively, we can often think of this as the complete answer to a question. For example: “How did the coin land?” has the answer-set {Heads, Tails}. For another: “How much charge does your phone have?” has the answer-set {100%, 99%, …, 1%, 0%}.
Bayesians then model the incorporation of evidence as follows. First, you begin with a probability distribution over all relevant possibilities. Then the true answer to the question comes in—Heads or Tails, as the case may be—and in each relevant possibility you update by conditioning on that true answer. What the true answer is depends on what possibility you’re in, of course—if the coin lands heads, you condition on Heads; if the coin lands tails, you condition on Tails.
Though often overlooked, models like this imply that your always going to answer the same question. It’s as if you’ve specified exactly what you’re going to pay attention beforehand—how the coin landed, in this case—and then only ever pay attention to that.
The above video shows how unrealistic this is. We can’t possibly specify exactly the question we’re going to pay attention to beforehand—there are too many things we might see, and too many questions we might ask about it. Instead, we have to reconstruct a (set of) question(s) to answer about our experience after we have the experience.
For example, I’m guessing you didn’t think beforehand “There might or might not be a Christmas tree, and I’m going to figure that out”. But of course, as soon as you saw the scene, you formulated the question and answered it in the affirmative.
Yet there were plenty more questions that you could have formulated but didn’t. For example, once you’d seen the Christmas tree you could’ve asked “Will the decorations on it change?”. If you had, you would’ve noticed that they did change—but you didn’t; instead you were only disposed to formulate that question if you spotted something odd about the Christmas tree.
Upshot: Unlike normal Bayesian models, limited agents need to formulate the questions to answer about their evidence post hoc, after it comes in. That opens up the possibility that which questions they answer might be correlated with what they see. What happens if they are?
Ideological Bayesians
Turn to Professor Polder.
To keep the model tractable, suppose there are just two possible questions you could ask about each comment he makes:
Qa = Is it aggressive? Answers: {aggressive, not-aggressive}
Qi = Is it insightful? Answers: {insightful, not-insightful}
So there are four possibilities for each comment: it’s aggressive and not-insightful (A¬I) it’s aggressive and insightful (AI), it’s not-aggressive and insightful (¬AI), or it’s not-aggressive and not-insightful (¬A¬I).
Let’s suppose, objectively, he’s 50%-likely to be aggressive and 50%-likely to be insightful in any given comment, and the two features are independent of each other. Thus, for each comment, the distribution among the four possibilities is uniform. Assume both fans and critics have priors for each comment that start like this:
This says, for instance, that they’re initially 25%-confident that the comment will be aggressive-and-not-insightful (A¬I), 25%-confident it’ll be aggressive-and-insightful (AI), and therefore 0.25+0.25 = 50%-confident it’ll be aggressive (A¬I or AI).
To ask a question is to notice which side of the partition you’re on. For example:
If the comment is aggressive and not-insightful (A¬I), and you ask only whether it’s aggressive (Qa), you learn only that he’s aggressive, i.e. “A¬I or AI”.
If the comment is aggressive and not-insightful (A¬I), and you ask only whether it’s insightful (Qi), you learn only that it’s not-insightful, i.e. “A¬I or ¬A¬I”
Given this, let’s start with a simple illustration of how selective attention to questions can lead to disagreement.
How do the fans and critics update from their prior to their posteriors? That depends on what happens—they learn different things in different worlds. Suppose his critics and fans have reliable, simple dispositions:
Critics’ dispositions: When his comments are aggressive, they always ask Qa, noticing that they’re aggressive. When his comments are not-aggressive, they always ask Qi—noticing whether they’re insightful or not.
Fans’ dispositions: When his comments are insightful, they always ask Qi, noticing that they’re insightful. When his comments are not-insightful, they always ask Qa—noticing whether they’re aggressive or not.
Given these simple dispositions, we can explicitly write what posteriors they end up with as a function of whether the comment is insightful and/or aggressive.
We can do this with a matrix: the first row says what their posterior is if the comment is aggressive-and-not-insightful (A¬I), the second says what it is if it’s aggressive-and-insightful (AI), etc.
Here’s the formalization of the critics’ dispositions:
What does this diagram mean? Here’s how to read it.
If it’s an aggressive comment (first two rows, i.e. A¬I or AI), all they notice is that it’s aggressive—so they condition on that, zeroing out the ¬A-possibilities, but remain 50-50 on whether it was insightful or not
If it’s not aggressive and insightful (third row, i.e. ¬AI), all they notice is whether it’s insightful—so they condition on it being insightful (AI or ¬AI), and remain 50-50 on whether it was aggressive.
If it’s not aggressive and not insightful (fourth row, i.e. ¬A¬I), all they notice is whether it’s insightful—so they condition on it being not-insightful (A¬I or ¬A¬I), and remain 50-50 on whether it was aggressive.
The critics are always conditioning on a truth, but which truth they condition on—what they notice—depends on what happens.
As a result—despite being Bayesians—their posteriors are biased. They start 50%-confident that a given comment is aggressive. But if it is aggressive, they’ll jump to 100% (since they’ll ask Qa), and if it’s not aggressive, they’ll remain at 50% (since they’ll ask a different question, Qi, instead). Thus their average posterior confidence in the comment being aggressive is 0.5*1 + 0.5*0.5 = 75%—since this is higher than their prior of 50%, they tend, on average, to become more confident it’s aggressive.
(Meanwhile, their average posterior in the comment being insightful is unbiased: 0.5*0.5 + 0.25*1 + 0.25*0 = 50%.)
We can do the same exercise with Polder’s fans. The difference is that when he’s insightful, they always notice that, whereas when he’s not-insightful, they instead pay attention to whether he was aggressive. Here’s the matrix representing their posteriors:
Again:
If it’s not-insightful and aggressive (first row, i.e. A¬I), they notice only that it’s aggressive.
If it’s insightful (second and third rows, i.e. AI or ¬AI), they notice only that it’s insightful.
If it’s not-insightful and not-aggressive (fourth row, i.e. ¬A¬I), they notice only that it’s not-aggressive.
As a result, they’re biased in favor of insight: their average posterior that it’s insightful is 0.25*0.5 + 0.5*1 + 0.25*0.5 = 75%. Meanwhile, their average posterior that it’s aggressive is 0.25*1 + 0.5*0.5 + 0.25*0 = 50%.
What happens?
As a result of these differing biases, our ideological Bayesians will polarize.
We can see this in a variety of ways. Suppose both fans and critics see 100 comments from Professor Polder, each independent and having the same (uniform) prior probability of being aggressive and/or insightful.
How do their estimates of the proportion of these 100 comments that were aggressive and were insightful evolve, as they observe more and more of them?
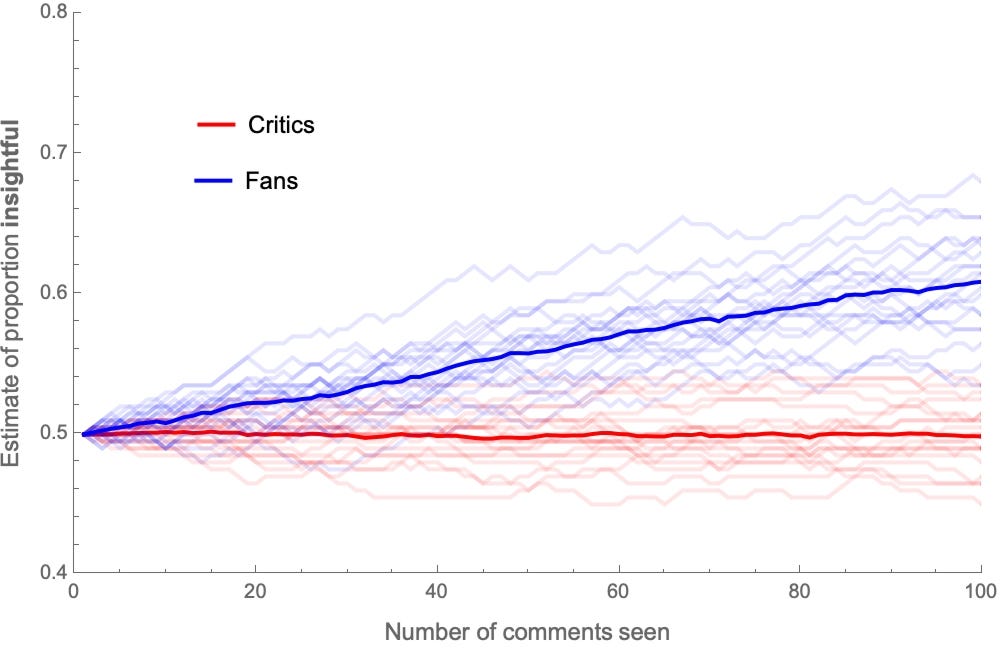
Here’s a graph of how—on average—their estimates of the proportion of aggressive comments out of 100 will evolve (thin lines are individuals; thick lines are averages):
After seeing all 100 comments, the average critic estimates that around 75% of them were aggressive, and the average fan estimates that around 50% of them were.
Similarly, here are the trajectories of estimates for the proportion of insightful comments:
After seeing all 100 comments, the average fan estimates that around 75% of them were insightful, and the average critic estimates that around 50% of them were.
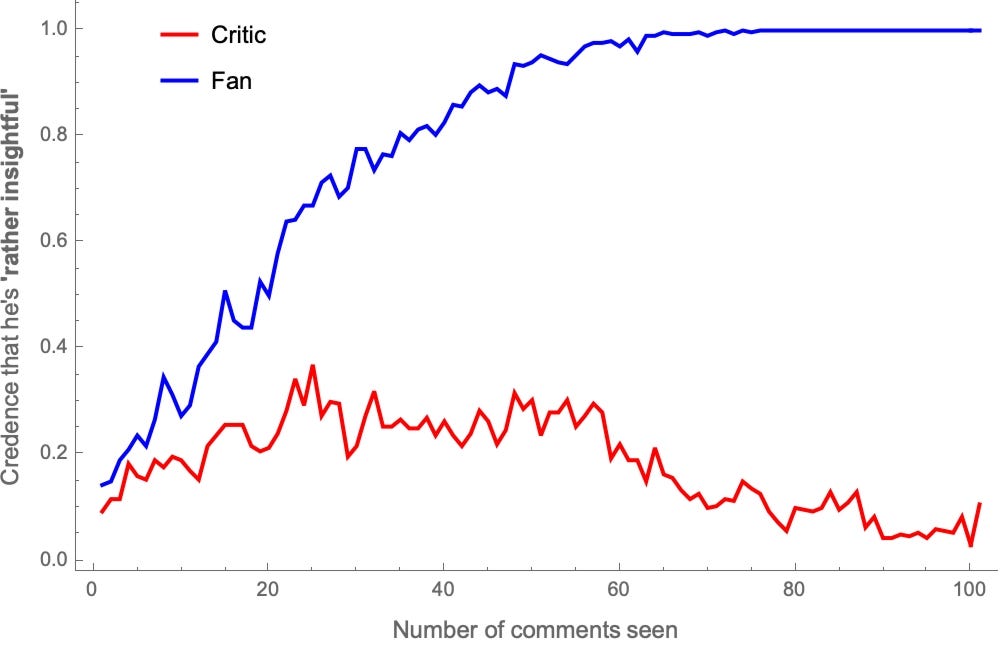
This divergences in estimates results in sharp disagreement in the probabilities they assign to particular claims. For example, let’s stipulate that Polder is “rather aggressive” if more than 55% of his comments are aggressive. Taking one representative fan and critic, here’s how their probabilities about whether he’s “rather aggressive” evolve as they see more comments:
After seeing the same 100 comments, the Critic is over 99%-confident that Polder is rather aggressive, while the the fan is around 10%-confident of that.
Likewise, stipulate that Polder’s “rather insightful” is more than 55% of his comments are insightful. Here’s how their probabilities in that evolve:
Upshot: When Bayesians are ideological in the simple-minded way described above, they can fall into polarization. The errors are systematic and predictable: the critics over-estimate the number of aggressive comments by 50% (75 rather than 50), and the fans over-estimate the number of insightful comments by 50% (75 rather than 50).
Of course, that simple-minded model was unrealistic: there was a perfect correlation between whether Polder was aggressive and/or insightful, and what questions his fans and critics paid attention to.
But nothing hinges on that—similar results emerge from imperfect correlations between what happens and what questions they ask. Call this stochastic updating.
For example, suppose his critics are simply a bit more likely to ask Qa if he is aggressive than to ask Qa if he’s not aggressive—meaning they’re a bit more likely to notice aggression than non-aggression. For instance: when he’s aggressive, they’re 90%-likely to ask Qa and 10%-likely to ask Qi; meanwhile, when he’s not-aggressive, they randomize: half the time they ask Qa, and the other half Qi.
Similarly, suppose his fans are a bit more likely to notice insight than non-insight. When he’s insightful, they ask Qi 90% of the time and Qa 10% of the time; but when he’s not-insightful, they randomize: half the time they ask Qi and the other half Qa.
These imperfect correlations lead to similar results. For example, here are their estimates for the proportion of aggressive and insightful comments, as they observe more comments:
And again—picking two representative fans and critics—here’s how their opinions on “rather aggressive” and “rather insightful” evolve:
What to make of this?
Upshot: Bayesians who always condition on truths but are “ideological”—in the sense that which questions they ask is correlated with what the truth is—can exhibit biases and fall into predictable polarization. They needn’t converge to each other, or to the truth. In fact, they’ll sometimes predictably go off the rails.
How robust are these results? I’m not sure—this is work in progress—but my conjecture is that introducing virtually any correlation between which questions you ask and what the truth is can be used to get similar results.
If that’s right, then the mere fact that we can’t specify all our questions about our evidence beforehand—but instead must do so post hoc, depending on what we see—seems enough to lead otherwise rational people into bias and polarization.
Crucial question: Will the disagreements persist, once ideological Bayesians find out about them? That depends heavily on what our they know about their own and others’ biases. Under ideal conditions, Bayesians can’t agree to disagree—but those ideal conditions require updating on the true cell of a constant partition, thereby ruling out the sort of correlations between truth and questions we’re studying here.
Of course, if our ideological Bayesians had perfect access to their own biases, they could (in principle) correct for them. But two points.
First, real people don’t have access to the details of their own habits of mind and attentional biases—such things are largely subpersonal and hard to detect.
Second, we’re modeling agents who aren’t able to update on their total evidence, so it’s no surprise that they don’t notice the patterns in their own biases—that would require them asking a different question about (their own responses to) their evidence.
So—though I don’t have anything like a proof of this, yet—I think on natural ways of expanding the model, the polarization that’s emerged will persist even once our ideological Bayesians learn of their disagreement.
Why does this matter?
First: my hunch is that this sort of mechanism helps explain why otherwise smart, diligent, and well-intentioned people so often fail to converge to the truth—even after extended exposure to similar evidence. We see this everywhere—among scientists, economists, political pundits, forecasters3, and (obviously) philosophers. Perhaps such disagreements are driven, in part, by the fact that they are systematically asking different questions about their (shared) evidence.
Second: the importance of selective attention for polarization is something “non-ideal” epistemologists, working on ideology, have been telling us for some time. The fact that this is demonstrably correct in a simple Bayesian setting suggests—to me, at least—that formal and non-ideal approaches to epistemology have more to learn from each other than is often thought.
What next?
This is a new project. What else should I read?
If you know of related work on Bayesian models of limited attention, please let me know!
If you have other reading suggestions about ideology and selective attention—from the critical-epistemology tradition, or cognitive science—please share them!
A similar mechanism to this post can result from limited memory—see this older post on why limited memory can prevent Bayesians from converging to the truth.
The idea that ideology' manifests as habits of mind and patterns of salience (among other things) comes from many authors in the feminist- and critical-epistemology tradition, especially authors like Mills (2007), Haslanger (2008, 2011, 2019, 2021), Siegel (2013), Munton (2023)—and goes back to at least DuBois (1903). Haslanger (2021) distinguishes between the sociological and critical uses of the term ‘ideology’: the former is understood descriptively, capturing the patterns that govern individuals’ perceptions and interactions; the latter is understood normatively, as the patterns that explain why individuals perpetuate oppression. (See also Geuss 1981.) I’m here using ‘ideology’ in a pared-down version of the descriptive sense, focusing on just the attentional—not necessarily normatively-loaded—effects of being “ideological”. This is for simplicity. What is the relationship between my model, and the broader debates about the notion of ideology? I don’t know. What do you think?
It’s sometimes said that Bayesian posteriors are “biased estimators” because they are biased toward the prior. Still, they are unbiased in at least two other important senses: (1) the average posterior equals the prior, and (2) conditional on the posterior estimate of X equalling t, the current best estimate for X is t.
For an extended discussion, see the recent existential risk persuasion tournament which found that superforecasters and AI experts failed to converge on estimates of AI risk, even after extended discussion and incentives for persuasion.








That's very cool. Is the idea of agents with limited resources updating on questions that are less fine-grained than the ones that their incoming evidence would allow them to answer already out there in the literature other places? Because even independent of the application to polarization, that's super interesting.
Thanks for writing this, very cool model! I'd be interested in seeing how much this changes if you extend the model to include others' beliefs as evidence (as you mention when talking about whether disagreements persist). In particular, it seems natural to think that Polder's fans and critics would find it at least a little useful to talk to each other -- since they're tracking different things -- and so even if they think the other is biased, presumably this might slow polarisation?
Excited to see your future work on this!