[Research conducted with Adam Bear.]
TLDR: You exhibit hindsight bias if learning that something happened increases your estimate for how likely you thought it was. The previous post argued that Bayesians should commit hindsight bias when—and only when—their priors are ambiguous, i.e. they’re unsure what their priors are. That prediction is easily testable. So we tested it. And it worked.
The Theory
You exhibit hindsight bias if learning that something happened increases your estimate for how likely you thought it was.
In the last post I made a theoretical argument: sensible Bayesians commit hindsight bias when (and only when) their priors are ambiguous—i.e. they are unsure what their own priors are.
What do I mean?
Sometimes our judgments under uncertainty are clear: we know exactly what we think. How likely do you think it is that this fair coin will land heads? That’s easy—50%. Not 60%, nor 40%, nor even 51%. You’re sure that you think it’s 50% likely.
Other times our judgments are ambiguous: we’re unsure what we think. How likely do you think it is that my brother owns at least 14 spoons? That’s hard. After all, your relevant evidence is an amorphous blob—base rates, cultural knowledge, hunches, what you know about me and can guess about my brother, etc. But I’m forcing you: name a number. Now.
‘50%’? Reasonable enough. Of course, I doubt that perfectly captures your opinion—you could just have easily have said 60% or 40%; you wouldn’t bet the farm that you’re exactly 50% (rather than, say, 52%). It’s unclear—ambiguous—what you think.
There are many models of ambiguity. The one I’ll use here—and will go to the mat for some other time—is higher-order probability. In clear cases, you have a subjective probability and are sure of what it is. In ambiguous cases, you have a subjective probability, but are unsure what it is.1
As we saw last time, this model predicts that—so long as you trust your judgment—hindsight bias is rational when (and only when) your priors are ambiguous. Why?
Think it through with our two cases.
News flash: the coin landed heads. How likely did you really think this was?
…50%. Obviously. That remains clear as day to you, since you know that all you knew was that it was a fair coin—it’d be nuts to commit hindsight bias here.
New news flash: my brother does own at least 14 spoons. How likely did you really think it was?
Of course, you know that you said ‘50%’. But you were never sure that this accurately captured your opinion—maybe you mis-stated it. And it was a weird question. Now that you think about it, you were sorta suspicious about the fact that I picked an oddly-specific number (14), and had a hunch that that might’ve been crucial. Maybe you were under-emphasizing that fact, and just rounding to ‘50-50’ since it’s a simple stand in for “I don’t know”. So maybe you were really more like 55% or 60%-sure…
That’s hindsight bias. Seems totally reasonable, doesn’t it? It should. Because it’s a theorem that whenever a Bayesian is unsure what their prior was (and thinks their prior is correlated with the truth), they should commit hindsight bias.
Upshot: this higher-order model of clarity and ambiguity makes a clear prediction.
The Hypothesis: people should commit hindsight bias in ambiguous cases, and they should not commit hindsight bias in clear cases.
The Experiment
That hypothesis is extremely testable. All we have to do is make scenarios where people’s priors should be clear vs. ambiguous, and then see if that modulates how often and how much they exhibit hindsight bias.2
Of course, we have to do this carefully. First, we train them:
They learn how to use the probability scale, and to distinguish their true probability (“what they really think”) from their guess about their true probability.3
They learn that they might be more or less confident that these guesses capture what they really think, and that re-thinking may lead them to revise their guess.
They answer comprehension questions, winnowing out those who don’t understand the setup or what we’re asking for.
Those who passed the comprehension and attention checks4 were then presented with 5 scenarios each, where they were asked to guess what their true probability was about something, and rate their confidence in their guess. These scenarios were randomized between clear and ambiguous versions.
Here’s a scenario from the clear condition:
Emily works on the 7th floor of the Eversure Insurance office building, where the programmers and accountants work. They employ 40 programmers and 60 accountants. Emily was selected randomly from this group.
Consider the hypothesis (H) that Emily is a programmer. How likely do you think this is?
And here’s the ambiguous variant:
Emily works on the 7th floor of the Eversure Insurance office building, where the programmers and accountants work. Please read the following vignette about her:
Emily sat at her workstation in the center of the bustling office, bathed in the soft glow of dual monitors. Her desk displayed neatly organized post-it notes and a large mug with mathematical jokes. Her fingers moved swiftly across a mechanical keyboard, the clicks melding into the office's ambient sounds.
She occasionally adjusted her black-rimmed glasses as she scrutinized the spreadsheet before her. She rubbed her temples as she worked—the numbers on the sheet blurring together. A worn comic book peeked out from under some papers, and a picture of her Yorkie Poodle smiled up at her from her desk.
Consider the hypothesis (H) that Emily is a programmer. How likely do you think this is?
The intuition: the clear version will lead people to guess that their true probability is 40%, and be confident in that guess—while the ambiguous version will lead them to guess some number or other, but be quite unsure in that guess.
Each participant gives us three data-points for each scenario they see. When they first see a scenario, they give us:
(1) Their guess for their true probability of H; and
(2) Their confidence (a slider from “unsure” to “certain”) that this guess captures what they really think. (We invert this to get their “ambiguity”: if they put the slider at 80%-confident, then their degree of ambiguity is 1 – 0.8 = 0.2.)
Afterward, they are told the outcome (“Emily is a programmer”), reminded what their prior guess about their true probabilities was, and then asked (3) whether—and if so, how—they’d like to revise their guess about their initial true probability.
What we care about is their hindsight shift—the difference between (3) and (1), i.e. their posterior guess about their prior in H minus their prior guess about their prior in H.5 If this difference is greater than 0, we code that as a “positive hindsight shift”.
We also want to know how this difference relates to (2) their self-reported ambiguity.
Predictions and Results
What happened? (Pre-registration here.)
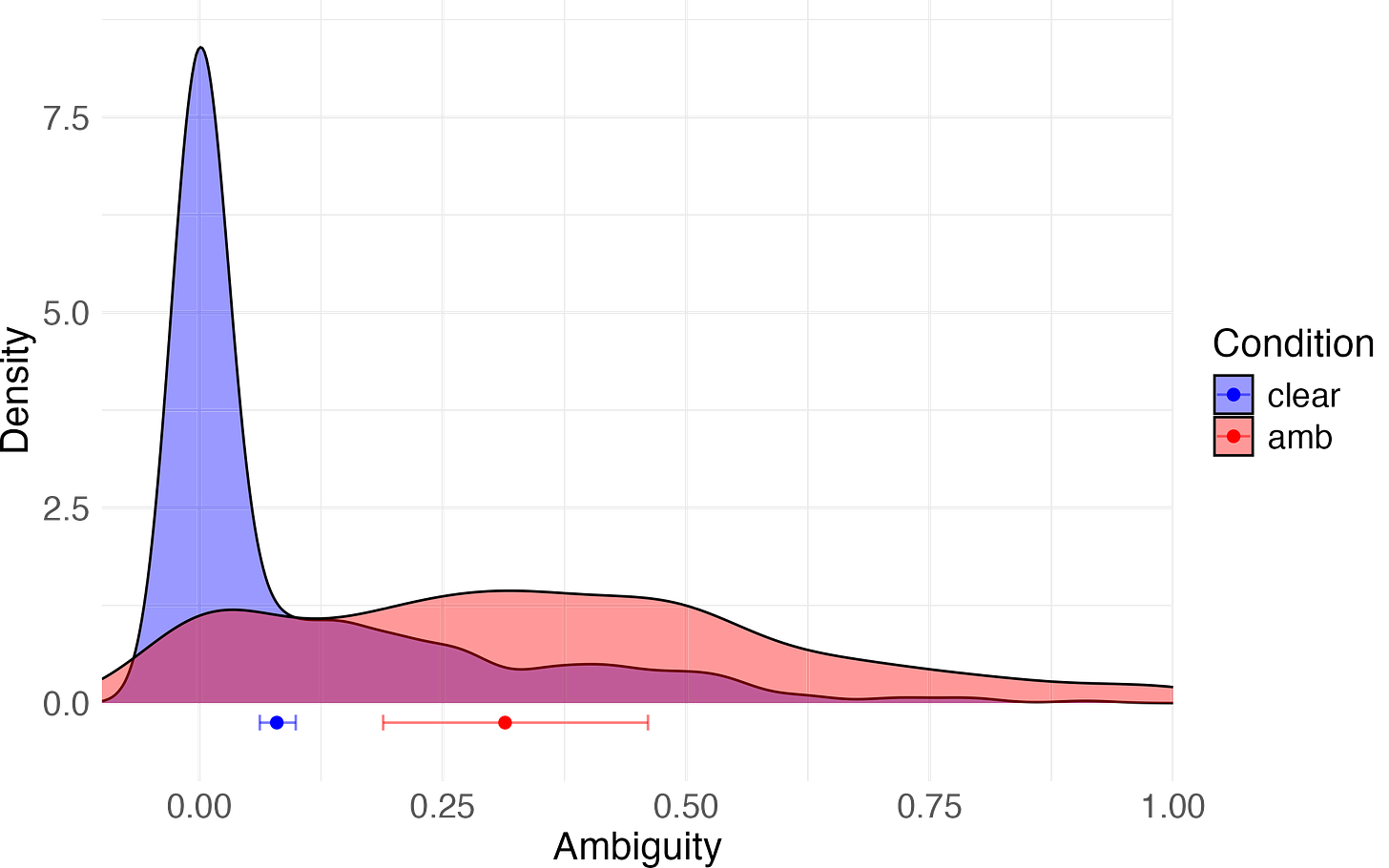
First, we needed to see if we successfully manipulated people’s self-reported degrees of ambiguity.
Prediction 1: The mean ambiguity will be higher in the ambiguous condition than in the clear one.
It was:
Next, we needed to test whether our manipulation of the degree of ambiguity affected how likely people were to exhibit positive hindsight shifts.
Prediction 2. People will be more likely to exhibit a positive hindsight shift in the ambiguous condition than the clear one.
They were. Model estimates said that people in the ambiguous condition were about 42%-likely to exhibit a positive hindsight shift, while those in the clear condition were about 5%-likely to do so:

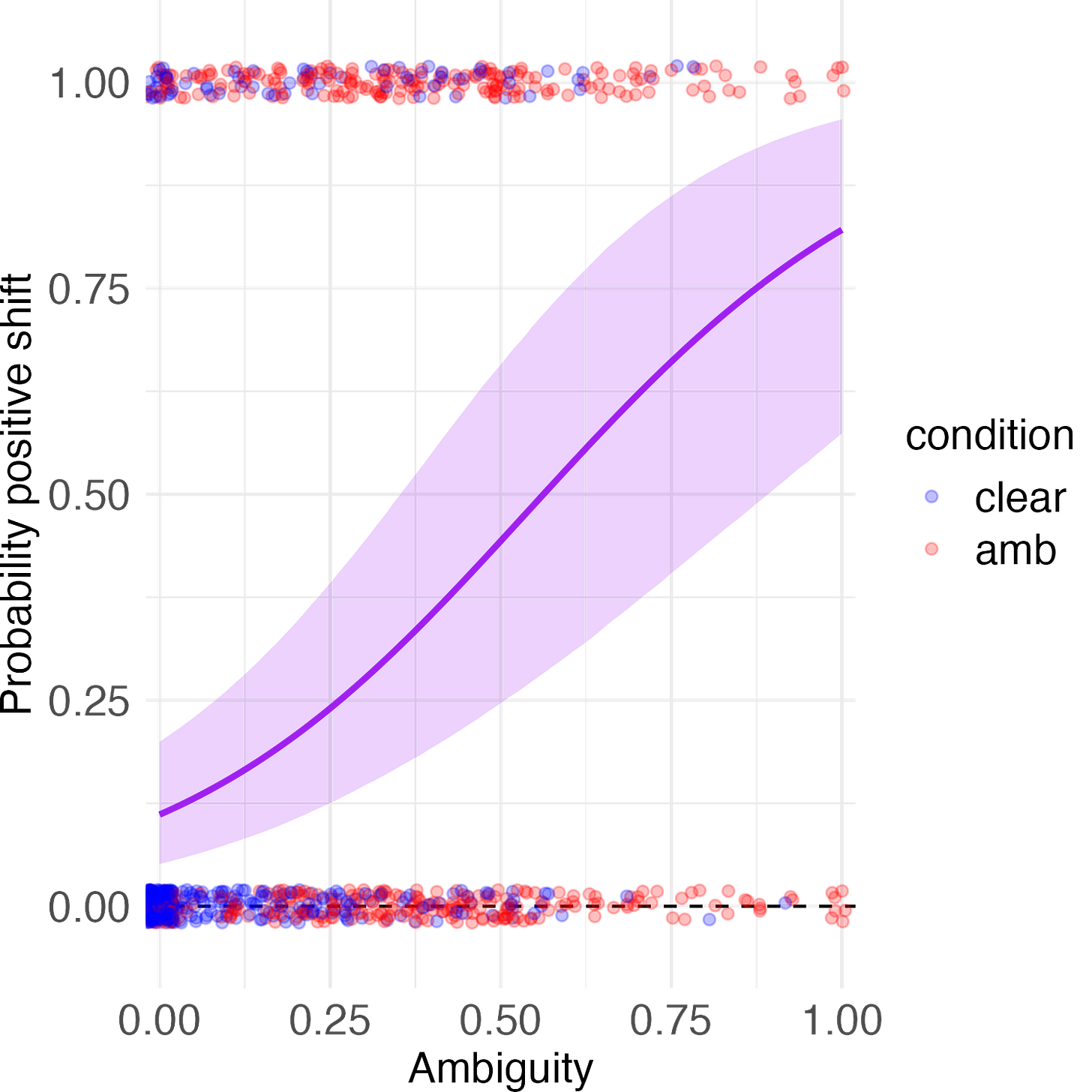
At a more fine-grained level, we wanted to see whether higher self-reported ambiguity was associated with an increase in the probability of a positive hindsight shift.
Prediction 3: Self-reported ambiguity will be positively correlated with the probability of exhibiting a positive hindsight shift.
It was. Model estimates said that as ambiguity rises from 0 to 1, the probability of a positive hindsight shift rises from around 11% to around 82%:
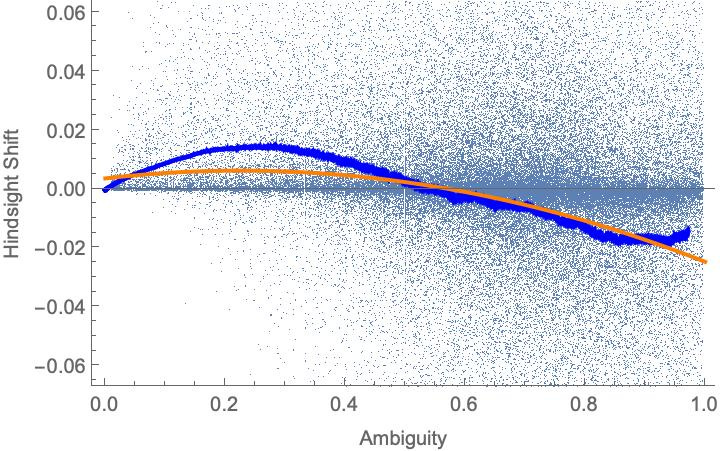
Next, the theory predicts that as people have more ambiguity in their judgment, their average hindsight shift should be greater. After all, if you’re pretty sure what your opinion is, there’s not very much latitude for your estimate to move—but if you have no idea, it can move a lot.
Prediction 4: Mean hindsight shift should increase with ambiguity.
It does. Indeed, the slope of the line is almost identical to that generated when we simulate random ambiguous models (orange line), without any model-fitting:

Finally, we wanted to test a risky theoretical prediction. Recall that the theory says that it is the combination of (1) uncertainty about your prior with (2) trust in your prior that leads to hindsight bias. If you don’t know what your prior is, but you think it’s uncorrelated with truth, then you shouldn’t exhibit hindsight bias.
Intuitively these two variables should be (negatively) correlated. In domains where you have expertise, you should both (1) be more confident in what you think, and (2) have more trust in your opinion. But in domains where you are (1) massively unsure what you think, you’re less likely to (2) trust your judgment.
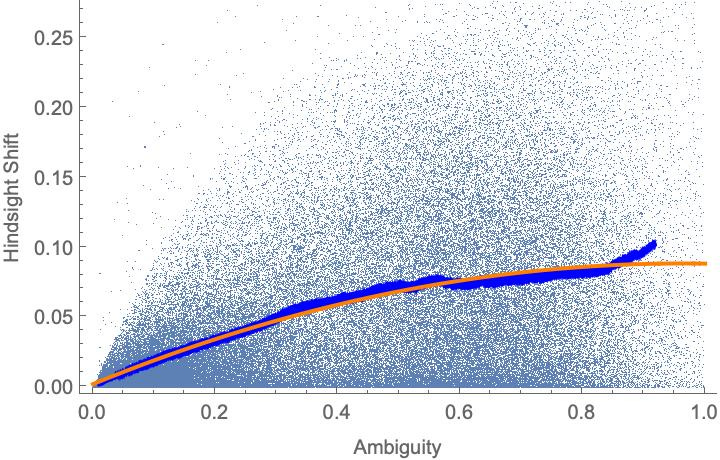
So, intuitively, the theory predicts a nonlinear relationship between ambiguity and hindsight shifts: you need some ambiguity in order to shift at all—but too much, and you’ll start to (on average) shift less.
This prediction is born out in simulations of random ambiguous models, however we set up the simulation. For instance, here are are random models with minimal rationality constraints on them, with a rolling average (blue line) and quadratic model (orange line) fit to the simulated data:
And here are random models with maximal rationality constraints on them:6
In both cases, the slope of the curve is positive while the curvature is negative (the orange lines are concave)—indicating that when ambiguity gets too high, hindsight shifts diminish, or even go negative.
This leads to a risky prediction:
Prediction 5: There will be a concave relationship between ambiguity and hindsight shift—with positive slope but negative curvature.
It worked.7 When we fit a quadratic model to the experimental data, the estimate for the slope is positive and for the curvature is negative. In fact—as you can see when we overlay the plots from the experiment and the simulations—the curves are strikingly similar:8
Upshots
What to make of all this?
The basic prediction of the model seems obvious (in hindsight!): if it’s clear what your prior was, you won’t commit hindsight bias; if it’s unclear, you might.
The data bears this obvious prediction out. Perhaps surprisingly, it also supports more subtle predictions about how the degree of ambiguity correlates with the likelihood and degree of hindsight shifts. Score one for Ambiguous Bayesianism.
Despite it’s obviousness, many prominent theories don’t explain the basic finding. Theories which say that people “anchor” on the truth, are motivated to see the world as predictable, engage in excessive “sense-making”, or misattribute fluency to predictability don’t clearly predict the effects of clarity and ambiguity.
Of course, there are other explanations that might be at play in our data. Maybe there’s more reputational leeway to shift in the ambiguous cases. Maybe the result is driven by objective probabilities in particular, rather than clarity more generally. Maybe something else.
More tests are needed. And we could use your help!
What questions do you have about the data? What are you most skeptical of? What follow-up experiments would you like to see? We’re all ears.
Yes, higher-order probability is mathematically and philosophically coherent—though there are many ways of doing it wrong. See e.g. Dorst et al. 2021 for how to do it right.
I don’t know of any paper that’s used a design like this. (Do you?) The closest I’ve found is Kneer and Skoczen 2023—Experiment 5 uses expert testimony to “stabilize” (i.e. clarify) the prior probability, and they find that it reduces hindsight bias.
This step was modeled off the methods of Enke and Graeber 2023.
189 of 400 people, i.e. 47%. The passing rate is unfortunately low, but it’s to be expected given the subtlety of the concepts involved, and is comparable to Enke and Graeber’s passing rate of 48%. Most who failed were not confused by the confidence-in-your-guess (higher-order probability) question, but instead by the hindsight question—they “revised” their guess toward the truth even in a case where it was stipulated that they remembered their prior exactly. No doubt this misunderstanding plays a role in some of the empirical support for hindsight bias; but as we’ll see—since we screened it out—it’s not the whole story.
Precisely, this is supposed to measure their E(P(H) | H) – E(P(H)), i.e. their posterior (upon learning H) expectation of their prior in H, minus their prior expectation of their prior in H.
For aficionados: the “minimal” constraint is New Reflection (from Elga 2013) while the “maximal” constraint is Total Trust—arguably the strongest plausible principle that permits ambiguity (from Dorst et al. 2021).
The 95%-credible interval for the slope is positive: [7.64, 27.07]. While the 95%-credible interval for the curvature isn’t completely negative (it’s upper-bound is 2.17); but the 89%-credible interval for the curvature is negative: [-21.94, -0.21].
Although it’s probably a coincidence, the slope and curvature parameters are remarkably close: the experimental estimates are 17.3 and -11.0 respectively, while the simulation estimates are 17.9 and -9.3, respectively. These simulations were in no way tuned to the data, but an attempt to generate fully-random models that satisfy the maximal rationality constraints.